Mit imaginären Zahlen kommen viele Schüler nur am Rande in Berührung. In der Regel haben sie schon mit den reellen Zahlen genug zu tun. Dennoch dürften die meisten irgendwann mal die Bekanntschaft mit der imaginären Einheit i machen, jener ominösen Zahl, die sich hinter der Wurzel aus -1 verbirgt. In den reellen Zahlen ist eine Wurzel aus einer negativen Zahl nicht definiert/erlaubt, die Mathematiker haben aber eine Erweiterung zu den reellen Zahlen geschaffen, die damit umgehen kann – die komplexen Zahlen! Hier gilt dann i2=−1.
 Das Rechnen mit komplexen Zahlen ist alles andere als intuitiv. Was bei der Addition noch harmlos aussieht, wird bei der Multiplikation schon kompliziert und beim Potenzieren dann gänzlich undurchsichtig. Insbesondere wenn man auf so verrückte Ideen kommt, wie mit der imaginären Zahl i zu potenzieren.
Das Rechnen mit komplexen Zahlen ist alles andere als intuitiv. Was bei der Addition noch harmlos aussieht, wird bei der Multiplikation schon kompliziert und beim Potenzieren dann gänzlich undurchsichtig. Insbesondere wenn man auf so verrückte Ideen kommt, wie mit der imaginären Zahl i zu potenzieren.
Was ergibt zum Beispiel i hoch i? Ehrlich gesagt entzieht sich das erst einmal der normalen Vorstellungskraft. Das Problem ist im wahrsten Sinne des Wortes sehr komplex 😉
Was ist das Ergebnis von ii
Die beste Antwort darauf gibt m. E. Matt Parker in seinem Youtube Channel Standup Maths. Mich hat das Ergebnis auf jeden Fall verblüfft.
Das ist schon ziemlich verwunderlich. Eine imaginäre Zahl mit sich selbst potenziert und als Ergebnis kommt eine reelle Zahl heraus. Im Beweis taucht übrigens auch die altbekannte Eulersche Identität wieder auf. Hier das Ergebnis in Kürze:
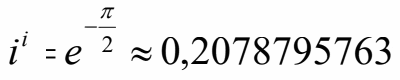
Achtung, wie schon im Video angedeutet, ist die vollständige Antwort auf diese Frage etwas komplexer. Aufgrund der 2πi-Periodizität der komplexen Exponentialfunktion existieren in Wirklichkeit unendlich viele Lösungen für i hoch i. Und die sind allesamt reell. Z.B. läge eine weitere Lösung von i hoch i bei 111.317778489…
Das Symbol Z steht für die Menge der ganzen Zahlen.
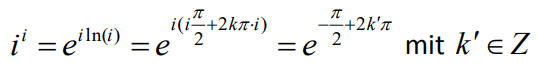
Sehr geehrte Damen und Herren,
das Ergebnis ist falsch.
Mit freundlichen Grüßen
M. Bauer
Falsch ist ein hartes Wort dafür. Unvollständig wäre wahrscheinlich treffender. Ich war so frei und habe die unterschlagenen weiteren Lösungen mal angehangen. Die Antwort fällt dann zwar komplexer aus, die Lösungen sind aber durch die Bank immer noch reell 😉
Ein Paradebeispiel von konstruktiver Kritik.
müsste der Term „2*pi*k'“ nicht noch ein „i“ enthalten, da e^(i*2*pi*n)=1 für n Element Z?