Der wohl bekannteste Lehrsatz der Mathematik dürfte der Satz des Pythagoras sein:
In einem rechtwinkligen Dreieck ist die Summe der Katheten-Quadrate gleich dem Quadrat der Hypothenuse.
Den meisten Menschen ist der Satz in der Kurzform a² + b² = c² geläufig, in dieser Form lässt er sich am leichtesten merken.
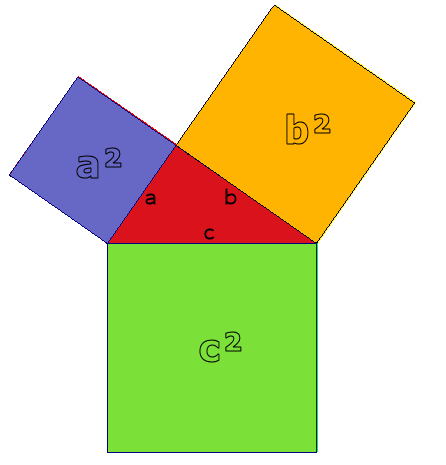
Eine Lösung für den Satz wäre z.B.: 3² + 4² = 5².
Es handelt sich hierbei um eine ganz besondere Lösung, weil alle Zahlen ganzzahlig sind. Es gibt übrigens unendlich viele solcher ganzzahligen Lösungen des Satzes des Pythagoras
(5² + 12² = 13², 6² + 8² = 10², 7² + 24² = 25²), die man auch Pythagoräische Zahlentripel nennt.
Beweise für diesen Satz gibt es wie Sand am Meer, aber nicht jeder Schüler wird jeden dieser Beweise gleich gut verstehen können. Und nicht jeder Beweis ist geeignet, den Sachverhalt leicht und verständlich herüber zu bringen. Mir ist damals im Studium ein Buch in die Hand gefallen, dass sich ausschließlich mit Beweisen des Satzes von Pythagoras befasst hat. Hundert Stück waren es an der Zahl. Ich denke, da sollte für jeden was dabei gewesen sein 
Bildquelle: Wikipedia/Pythagoras
