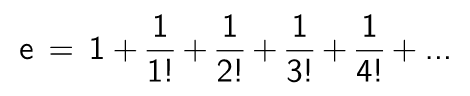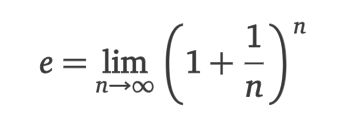Die Eulersche Zahl e

Vielleicht die wichtigste Zahl / Konstante in unserem Leben, nicht nur in der Mathematik, ist die so genannte Eulersche Zahl e = 2,718281828… . Betrachtet man die ersten Stellen von e, so würde man fast vermuten, die Zahl sei periodisch. Aber weit gefehlt, die Mathematiker konnten beweisen, dass es sich bei e nicht um eine rationale Zahl handelt. Das zu Beweisen war alles andere als trivial.

e = 2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 …

Leonhard Euler gelang im Jahr 1737 das Kunststück, die Irrationalität von e zu beweisen. Die Zahl wird ihm zu Ehren deshalb auch Eulersche Zahl genannt. Aber nicht nur aufgrund seines Beweises hat sich Euler den Ruhm verdient, er war auch der erste Mensch, der die Zahl mit dem Buchstaben e belegt hat. Witzigerweise passt das e sehr gut zu seinem Nachnamen, die Namensgebung hatte aber wahrscheinlich eher mit der Nähe zur Exponentialfunktion zu tun. Dass e auch noch transzendent ist, das war noch eine Stufe schwieriger zu beweisen und gelang erst im Jahr 1873 dem französischen Mathematiker Charles Hermite.

Die Eulersche Zahl stellt auf der einen Seite die Basis des natürlichen Logarithmus ln = log_e dar und bildet auf der anderen Seite auch die Basis für die natürliche Exponentialfunktion x -> e^x. Die Funktion e^x ist dabei ein ganz besonderer Fall einer Exponentialfunktion a^x, bei der die Funktionswerte und die jeweiligen Ableitungen miteinander übereinstimmen. Diese Eigenschaft macht die Zahl e und deren zugehörige Exponentialfunktion e^x für die Mathematik zu einem ganz speziellen und sympathischen Element, da damit zusammenhängende Integrale und Differentiale deutlich einfacher zu handhaben sind.

Einfache Formeln zur Berechnung der Eulerschen Zahl

Die Mathematik kennt Unmengen an Formeln zum Berechnen der Zahl e. Die eleganteste und natürlichste Formel dürfte die folgende, von Leonhard Euler entdeckte unendliche Reihe sein:

Eine ebenfalls sich relativ natürlich entwickelnde Formel basiert auf dem Grenzwert einer ins Unendliche fortgeführten Zinseszins Berechnung:

Ähnlich wie bei der Zahl Pi gibt es auch einen Wettbewerb rund um das Memorieren der Stellen von e. Mit 10.000 Nachkommastellen stellte der Inder Akshat Khandal im Jahre 2018 den Weltrekord im Auswendig Aufsagen der Ziffern von e auf.

Die Eulersche Zahl und die e-Funktion

Die Zahl e wird in der Mathematik selten alleine, sondern fast immer mit Bezug zum natürlichen Logarithmus ln(x) und insbesondere zur natürlichen Exponentialfunktion e^x gebraucht. Man bezeichnet e^x auch gerne als die e-Funktion. Gerade in der Physik sind viele Formeln mit dieser Funktion gespickt. Sie taucht z.B. auf bei Wachstumsproblemen, aber auch überall dort wo es um Schwingungen geht und gerne auch im Rahmen von Wahrscheinlichkeiten.

Die eulersche Zahl e in Alltag und Natur

Auch aus Biologie und Epidemiologie ist die e-Funktion nicht wegzudenken – die Corona Pandemie hat uns das ganz deutlich ins Gedächtnis gerufen. Wobei in diesem Fall neben dem exponentiellen Wachstum auch noch das logistische Wachstum ins Spiel kommt. Denn im Gegensatz zur Mathematik sind im realen Leben und in der Natur die Ressourcen nicht unendlich, daher gibt es am Ende meist einen Dämpfer oben drauf 😉

Die Zahl e taucht in Alltag & Natur öfter auf, als man denkt. Klassiker ist der Verlauf des radioaktiven Zerfalls. Und selbst die Abkühlung einer Tasse Kaffee wird mit Newtons Abkühlungsgesetz und damit mit einer e-gespickten Formel beschrieben. Und auch die Gaußsche Normalverteilung lebt im Kern von der e-Funktion und steckt in Unmengen von Statistiken. Zum Beispiel in der Verteilung von Intelligenz, Körpergrößen, Armlängen oder Schuhgrößen.

Witzig ist auch der folgende Fall einer fixpunktfreien Permutation. Die Gäste einer Hochzeitsgesellschaft geben ihre Hüte an der Garderobe ab. Die Garderobiere gibt den Gästen die Hüte am Ende der Veranstaltung per Zufallsprinzip zurück. Wie hoch ist die Wahrscheinlichkeit, dass kein Gast seinen eigenen Hut zurück bekommt? Die Wahrscheinlichkeit nähert sich sehr schnell dem Wert 1/e = 0.3678794… an. Man spricht in diesem Zusammenhang oft auch von der 37% Regel.

Wert der Eulerschen Zahl und Rechnen mit der e-Funktion auf dem Taschenrechner

Natürlich findet man die Zahl e und die Funktion e^x auf jedem besseren Taschenrechner. Dabei liegt insbesondere die e-Funktion etwas versteckter – unter der ln-Funktion.

Diese Funktion zum Berechnen des natürlichen Logarithmus hat (aus welchen Gründen auch immer) Vorrang auf den meisten Rechner-Tastaturen. Um die natürliche Exponentialfunktion aufzurufen, muss in der Regel eine Umschalttaste gedrückt werden.

Neben dem Rechner bzw Taschenrechner rechnen viele Schüler und Studenten auch gerne mit Microsofts Excel herum. Hier wird die e-Funktion über den Befehl EXP() ausgeführt. Der Wert der Zahl e ergibt sich demzufolge mit Hilfe des Ausdrucks EXP(1).

FAQ – Fragen rund um die Eulersche Zahl / e-Funktion

Was ist e?

Die eulersche Zahl e ist eine sowohl irrationale als auch transzendente reelle Zahl. Benannt wurde sie nach dem Mathematiker Leonhard Euler. In der Regel tritt e im Zusammenhang mit der natürlichen Exponentialfunktion e^x bzw. dem natürlichen Logarithmus ln(x) auf – deren beider Basis sie ist.

Wie ist die eulersche Zahl definiert?

Man kann die eulersche Zahl auf verschiedene Arten definieren. Als Grenzwert einer speziellen Zinseszins-Formel oder als unendliche Reihe e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + … oder als jene Basis einer Exponentialfunktion, bei der alle Funktionswerte mit dem Wert der Ableitung übereinstimmen.

Wieviele Nachkommastellen hat die Zahl e

Aufgrund ihrer Irrationalität besitzt die Eulersche Zahl e unendlich viele Nachkommastellen. Davon bekannt sind aktuell 12 Billionen Stellen, veröffentlicht von David Christle am 12. Juli 2020.

Kann die e-Funktion Null werden?

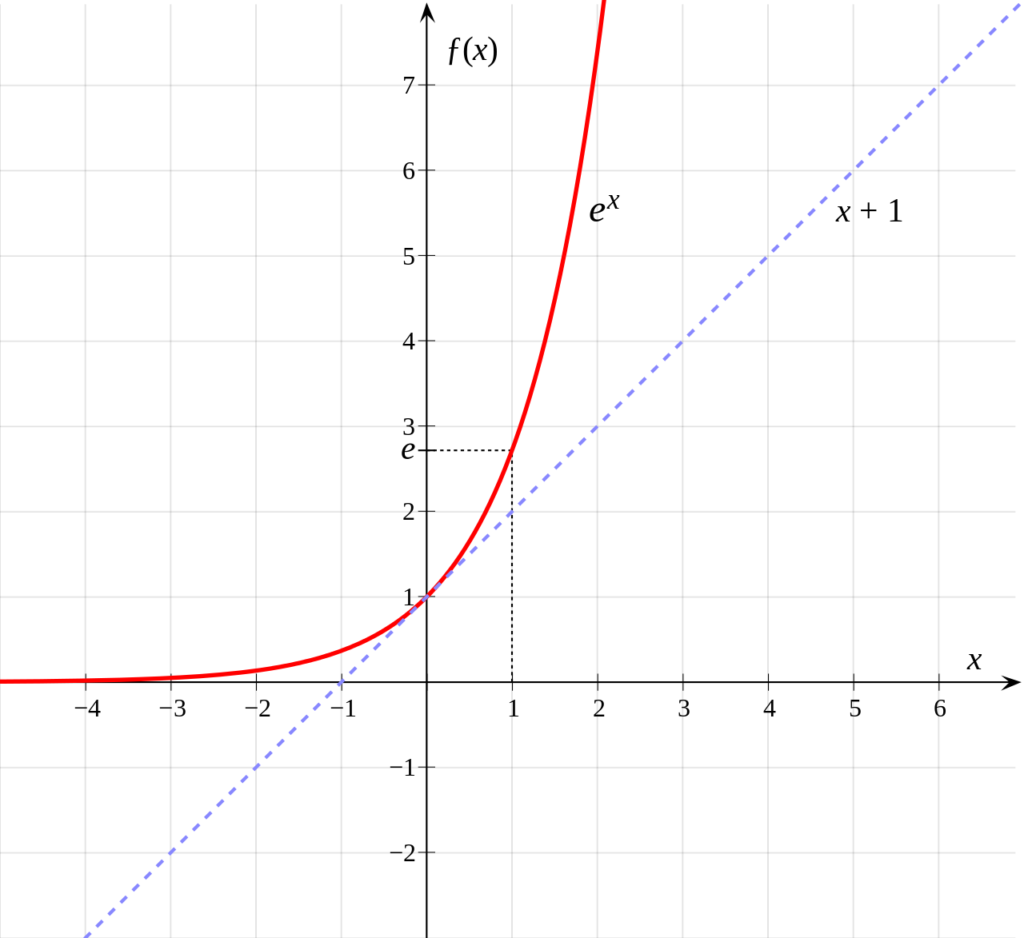
Bei der e-Funktion handelt es sich um eine streng monoton steigende Funktion, für die alle Funktionswerte größer als Null ( e^x > 0 ) sind. Insbesondere ist die Umkehrfunktion ln(x) an der Stelle Null ( ln(0) ) nicht definiert. Die e-Funktion berührt die x-Achse sozusagen erst im Unendlichen.
Sieht man auch schön am Funktionsgraphen der e-Funktion.