Einer der ältesten Sätze der Mathematik (ca. 600 v. Chr.) und damit noch etwas älter als der Satz des Pythagoras, ist der Satz des Thales. Der Satz wird dem griechischen Astronomen, Mathematiker und Philosophen Thales von Milet (624 – 547 v. Chr.) zugeschrieben und besagt kurz und knapp das Folgende:
Alle Dreiecke in einem Thaleskreis sind rechtwinklig.
Unter einem Thaleskreis versteht man einen Halbkreis. Damit kann der Satz auch so formuliert werden: „Alle Winkel über einem Halbkreisbogen sind rechte Winkel.“
Beweis zum Satz des Thales
Für den Beweis des Satzes von Thales benötigt man eigentlich nur zwei ganz elementare geometrische Hilfssätze.
- Die Winkelsumme in einem Dreieck ist 180 Grad.
- Die Basiswinkel in einem gleichschenkligen Dreieck sind gleich groß.
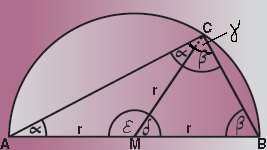
Betrachten wir das Dreieck ABC und den Radius MC, so erkennen wir, dass MC das große Dreieck in zwei gleichschenklige Teildreiecke zerlegt. Die Winkel im Dreieck ABC lassen sich wie folgt darstellen: α + β + γ = 180 Grad. Da sich der Winkel γ aus den beiden Basiswinkeln α und β zusammen setzt, erhalten wir: α + β + α + β = 180 Grad.
Eine einfache Umformung macht daraus 2*(α + β) = 180 Grad, woraus unmittelbar α + β = 90 Grad folgt. Der gesuchte Winkel γ = α + β ist damit ein rechter Winkel.
q.e.d.
Beweise für den Satz des Thales gibt es einige im Internet, u.a. auch in Form von Videos. Das hier dauert keine 3 1/2 Minuten. Schaut einfach mal rein.
In der Schule wird der Satz des Thales normalerweise in der 7. – 8. Schulklasse eingeführt bzw. abgehandelt. Auch die Umkehrung des Satzes gilt. Die Hypotenuse wäre dann der Durchmesser des zu konstruierenden Halbkreises und der Punkt C würde den Kreisbogen berühren. Der Thaleskreis taucht in der Geometrie oft im Zusammenhang mit Aufgaben zur Bestimmung von Kreistangenten auf.
Typische Anwendungsfälle im Mathematik Unterricht sind Aufgaben zur Konstruktion von rechtwinkligen Dreiecken mit Hilfe von Zirkel und Lineal. Oder geometrische Beweise, in denen Thales als Hilfssatz zu weiteren Schlussfolgerungen führt. Im Alltag findet der Satz des Thales hingegen kaum Anwendung. Die rutschende Leiter wäre eine der wenigen Thalessatz-Anwendungen mit einem gewissen Praxisbezug.
Die rutschende Leiter
An der Wand lehnt eine Leiter. In der Mitte der Leiter steht eine Person. Welche Bahn beschreibt der Leiter-Mittelpunkt, wenn die Leiter zu Boden rutscht?
Der Thales Satz war schon vorher bei den alten Ägyptern und Babyloniern bekannt. Doch Thales von Milet hat den ersten öffentlichen Beweis dafür erbracht. Noch populärer als der Satz von Thales ist der Satz von Pythagoras. Auch dieser Lehrsatz ist Teil der Geometrie, auch hier dreht sich alles um Dreiecke und rechte Winkel, doch interessieren in diesem Fall keine Kreise sondern Seitenlängen, Quadrate und Flächen.
Ausgangsmaterial für die Grafik: Wikipedia / Hubi / Thalesbeweis
Die Konstruktion der Kreistangenten ist eine praktische Anwendung zur Berechnung des sichtbaren Ausschnittes eines kreisförmigen Objektes von einem Punkt P aus. Der am Mittelpunkt des Kreises mit der Kathete des konstruierten Dreieckes zu berechnende Winkel ist verdoppelt ein Maß für den sichtbaren Kreissektor.