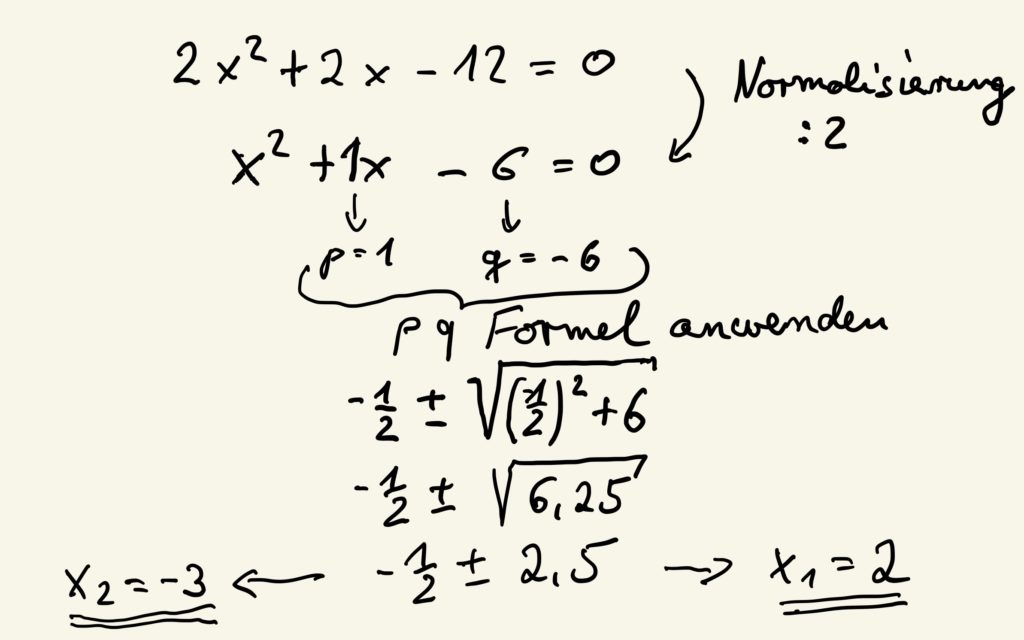Es gibt verschiedene Methoden, eine quadratische Gleichung zu lösen bzw. die Nullstellen einer quadratischen Gleichung zu berechnen. Sei es die Mitternachtsformel, der Satz von Vieta oder die an ein Ratespiel erinnernde Linearfaktor-Zerlegung. Doch die wohl populärste Lösungsmethode dürfte die Berechnung mit Hilfe der pq-Formel sein.
Im Wesentlichen besitzt eine quadratische Gleichung die folgende Form bzw. kann in solch eine allgemeine quadratische Gleichung umgeformt werden: ax2 + bx + c = 0. Die reellen Zahlen a, b und c sind beliebige Koeffizienten, wobei a nicht 0 sein darf, weil ansonsten das Quadratische Element verloren gehen würde. Unter diesen Voraussetzungen kann die obige quadratische Gleichung von der allgemeinen Form in die klassische Normalform x2 + px + q = 0 überführt werden.
Lösung mit Hilfe der pq-Formel
Für diese vereinfachte Form einer quadratischen Gleichung gibt es jetzt eine relativ einfache Lösungsformel – die sogenannte pq-Formel:
![]()
Durch Einsetzen von p und q in die Formel erhält man i.A. zwei verschiedene Lösungen.
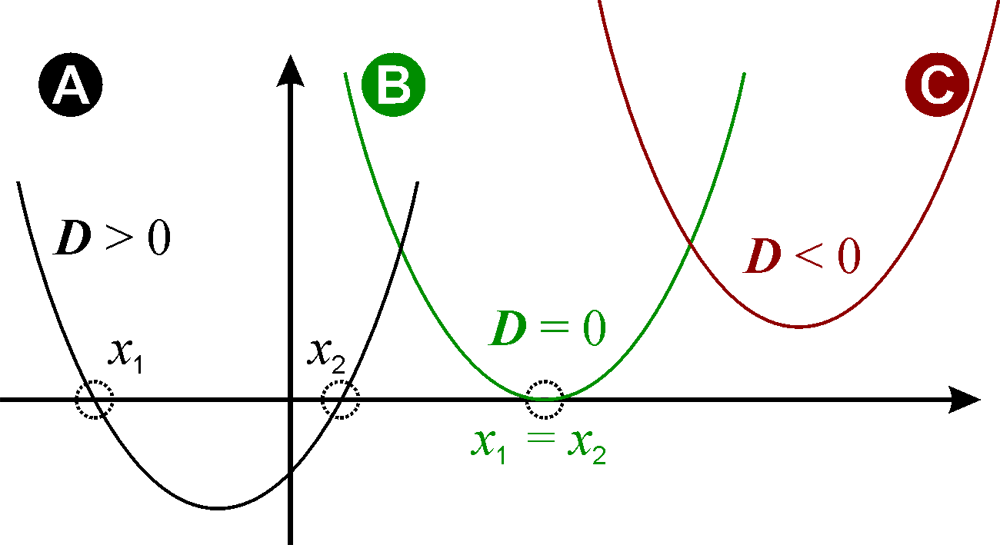
Je nach dem Wert des Wurzel-Terms sind aber auch nur eine oder auch gar keine Lösung möglich. Das Innere des Wurzel-Terms wird deshalb (bezeichnender Weise) Diskriminante genannt.
Eine Diskriminante größer als Null bedeutet, es existieren zwei unterschiedliche Lösungen in den reellen Zahlen (Kurve A). Sollte die Diskriminante gleich Null sein, liefert die pq-Formel mit -p/2 nur eine Lösung (Kurve B). Man spricht in diesem Fall auch gerne von einer doppelten Nullstelle. Sollte die Diskriminante gar einen negativen Wert annehmen, dann sind wir in den reellen Zahlen leider am Ende, da das Radizieren (Wurzelziehen) nur für nicht negative reelle Zahlen erlaubt ist (Kurve C). Die Parabel schneidet in diesem Fall die x-Achse nicht.
Kaum zu glauben, aber wahr. Es gibt mit den komplexen Zahlen eine Erweiterung der reellen Zahlen, die auch Lösungen quadratischer Gleichungen mit negativer Diskriminante erlaubt. Dieser „imaginäre“ Zahlenbereich begegnet einem aber meist erst im Rahmen des Studiums oder der Berufsausbildung. Genau betrachtet gibt es gemäß dem Fundamentalsatz der Algebra in den komplexen Zahlen zu jedem Polynom auch mindestens eine Nullstelle.
PQ Formel Song
Nicht nur für die Binomischen Formeln hat der Dorfuchs einen Mathe-Song getextet, er hat auch einen sehr populären p-q Formel Song produziert. Das Youtube Video dazu wurde schon mehr als 2 Millionen mal abgespielt und befasst sich mit der Anwendung und Herleitung der pq-Formel zum Lösen quadratischer Gleichungen. Dieser mathemusikalische Ohrwurm hilft euch, die pq-Formel besser zu merken und zu verstehen.
PQ-Formel Rechner
Im Internet gibt es einige PQ-Formel Rechner, mit deren Hilfe man nicht nur die Ergebnisse ausrechnen, sondern sich auch die Rechenschritte inklusive Umformungen auflisten lassen kann. Zum Lernen und Rumexperimentieren ist das ganz nett, ich rate aber davon ab, sich auf solche Rechner zu verlassen. Lieber ein paar Aufgaben händisch lösen, als sich auf eine künstliche Intelligenz zu verlassen. Hat der Rechner keinen Strom oder fehlt ihm die Online Anbindung, dann ist Schluss mit Lustig. Dagegen habt ihr euer Gehirn immer dabei und könnt eure Lösung hoffentlich einfach heraus schütteln. Denn spätestens bei der nächsten Mathe-Arbeit hilft euch nur noch euer eigener Verstand 😉
Beispiel zur pq-Formel
Um die Formel anwenden zu können, ist es notwendig, die Gleichung gleich zu Beginn zu normalisieren. Das sorgt dafür, dass der Faktor vor dem X2 zu einer 1 mutiert (umgewandelt wird). Der Trick bei der Normalisierung besteht darin, dass sich die Nullstellen der Gleichung nicht ändern. Die Kurve wird lediglich um den Normalisierungsfaktor gestaucht oder gestreckt, die Nulldurchgänge bleiben jedoch genau an ihrer ursprünglichen Stelle liegen.