Die für mich verblüffendste und faszinierndste Formel der Mathematik ist die auf Leonard Euler zurück zu führende Gleichung eπi +1 = 0. Es handelt sich um einen Spezialfall der Eulerschen Identität. Ihr könnt sie hier in voller Schönheit bewundern:
Das folgende Video versucht die Gleichung e hoch πi + 1 = 0 auf anschaulich Art und Weise zu erklären. Und das ist gar nicht mal so einfach. Denn die komplexen Zahlen und ihre Rechenregeln sind für Nicht-Mathematiker reichlich abstrus und kompliziert 😉
Überhaupt gibt es ziemlich seltsame Zusammenhänge in der komplexen Mathematik. Betrachten wir nur eπ = 23.1406926327792690…, da kämen wir nie auf die Idee, dass so etwas Krummes mit i potenziert so eine simple Zahl als Lösung hat.
Es ist schon schwer genug, sich so etwas wie das Potenzieren mit i vorzustellen. Noch schräger wird es aber, wenn wir i mit sich selber potenzieren. Verblüffenderweise erhalten wir ii = e -π/2 = 0.207879576350… und damit eine reelle Zahl als Ergebnis einer überaus komplexen Rechnung. Voll schräg 😉
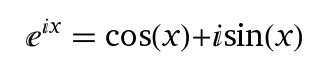
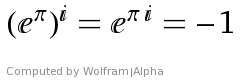
Die Eulersche Formel e π*i=-1 ist mathematischer Blödsinn!
Die Eulersche Formel e π*i=-1 (1)
ist mathematischer Blödsinn! Denn es gilt mit dem Quadrieren der Gleichung (1):
e π*i*2=1! (2)
Logarithmiert man nun beide Seiten mit dem natürlichen Logarithmus, dann ergibt sich
ln [e π*i*2]=ln 1! (3)
Ln 1 ist aber Null! Damit kann nach den Logarithmen-Gesetzen formuliert werden:
π*i*2* ln e =0. (4)
Damit gilt schlussendlich mit i=√-1 und dem nochmaligen Quadrieren beider Seiten
4* π²≠0! (5)
Damit ist 1= 0, (6)
was natürlich mathematischer Schwachsinn ist!
Daraus lässt sich logisch implizieren, dass Euler einer der größten Scharlatane in der Geschichte der Mathematik war! Dies lässt sich übrigens anhand einer (mathematischen) Anekdote, die sich am Hof von Katharina der Großen in Petersburg zugetragen haben soll, zweifelsfrei belegen. Denn Euler zu Diderot (und zum Hofe von Katharina der Großen): „a*bπ=x – darum existiert Gott“. Diderot soll daraufhin fluchtartig den Hof verlassen haben (nach Wikipedia).Die Formel ist natürlich absoluter Blödsinn. Daher an die Leserschaft die Mahnung und Warnung: Immer schön aufpassen bei ganz komplizierten mathematischen Formeln, Zusammenhängen und Abhandlungen! Denn: Genialität beweist sich immer in Einfachheit, weil die Materie einfach strukturiert ist!
Netter Versuch. Dir ist aber schon klar, dass du eine komplexe Exponential-Funktion mit einer reellen Logarithmus-Funktion umzukehren versuchst.
Wahnsinn, welch Blödsinn im Internet scheinbar auch möglich ist!!!